Разработка уроков по теме "Неполные квадратные уравнения"

За каждое правильно решенное задание команда получает по одному жетону).

На работу вам 10 минут.

Решить неполные квадратные уравнения:

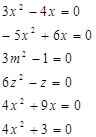
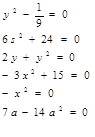
3.5.1 Проверка ответов.

4. Итог урока

Что мы повторили?

Сейчас посмотрим, какая команда набрала больше жетонов (за первое место грамота). Теперь капитаны каждой команды должны оценить работу каждого члена команды.

Урок-практикум по теме "Неполные квадратные

уравнения"

Тип урока: закрепление и проверка знаний.

Цель: закрепить и проверить знания по теме "Неполные квадратные уравнения", развивать математическую речь, внимание, воспитывать самостоятельность, интерес к предмету.

Оборудование: карточки с заданиями для самостоятельной работы, листочки для математического диктанта.

Ход урока:

Организационный момент.

Сообщение темы и цели урока.

Актуализация знаний.

3.1 Математический диктант (на листочках).

Какое уравнение называют квадратным уравнением?

Какое уравнение называют неполным квадратным уравнением?

Какие виды неполных квадратных уравнений бывают?

Сколько корней может иметь неполное квадратное уравнение ?

Сколько корней может иметь неполное квадратное уравнение ?

Сколько корней может иметь неполное квадратное уравнение ?

3.2 Проверка математического диктанта (меняются листочками).

Работа по теме урока.

4.1 Решение неполных квадратных уравнений.

4.1.1 Решение у доски:

а)

б)

4.1.2 Самостоятельная работа (по вариантам). На работу 4 минуты. Кто решит первым запишет свой ответ на доске.

1 вариант:

2 вариант: .

4.1.3 Проверка самостоятельной работы: сверка с доской.

4.2 Докажите, что:

а) числа 5 и - 5 являются корнями квадратного уравнения ;

б) числа о и - 7 являются корнями квадратного уравнения

Под буквой а решает 1 ученик с обратной стороны доски, под б - 2 ученик, остальные решают самостоятельно в тетрадях.

4.2.1 Проверка: самопроверка.

5. Самостоятельная работа на 1 вариант.

Решаем до конца урока и сдаем тетрадь на проверку.

1. Найти корни уравнения:

а) ;

б) .

2. Решите уравнение:

а) ;

б) .

3. Какие из следующих уравнений являются неполными? В Случае неполного уравнения найдите его корни.

а) ;

б) ;

в) ;

г) .

4. Найдите сумму корней неполного уравнения .

6. Итог урока.

Баллы по заданиям: за каждое правильно решенное задание 1 балл.

Итоговая шкала оценок:

9б. - "5"

7-8 б. - "4"

5-6 б. - "3"

Менее 5 б. - "2"

Анализ уроков по теме "Неполные квадратные уравнения"

В связи с тем, что по тематическому планированию изучение темы "Квадратные уравнения", начинается с рассмотрения вопроса о неполных квадратных уравнениях, были разработаны и апробированы уроки именно по этой теме: урок - лекция, урок - игра и урок - практикум.

Цели и задачи уроков выполнены. Все учащиеся были хорошо подготовлены к урокам. Они с интересом работали на уроках, этому служит эмоциональная речь учителя, приветливое отношение, поддержка отстающих. Ученики внимательны, сосредоточены.

Читайте также:

Методические основы обучения лексическому аспекту иностранного языка
Лексика в системе языковых средств является важнейшим компонентом речевой деятельности: аудирования и говорения, чтения и письма. Это определяет ее важное место на каждом уроке иностранного языка, и формирование лексических навыков постоянно находятся в поле зрения учителя. Что такое лексика? Лекси ...

Организация профессиональной ориентации учащихся 9-х классов в условиях школ и межшкольных комбинатов
Для формирования внутренней готовности учащихся к осознанному и самостоятельному определению в выборе профессии, корректировке и реализации своих профессиональных планов в условиях школ и межшкольных комбинатов проводится профессиональная ориентация учащихся. Рассмотрим особенности той и другой сто ...

Методика проведения формирующего эксперимента
В ходе констатирующего эксперимента были зафиксированы данные, которые стали исходными для нашего формирующего эксперимента. Главная цель на этом этапе - проверка эффективности применения дидактических игр для развития интеллектуальных способностей дошкольников. При поиске оптимальных методов и сре ...