Теоретический анализ основных математических понятий

Переместительное свойство умножения в начальных классах формулируется так: «От перестановки множителей произведение не изменится». Данное свойство широко используется при составлении таблицы умножения однозначных чисел [18,142-144].

Рассмотрим задачу, которую решают младшие школьники, приступая к изучению действия деления: «8 апельсинов разложили на тарелки, по 2 апельсина на каждую. Сколько раз по 2 апельсина положили? Сколько тарелок потребовалось?

Ответ на вопрос задачи находится при помощи деления: 8:2=4.

Проанализируем решение этой задачи. В задаче рассматривалось множество, в котором 8 элементов. Оно разбивается на подмножества, в каждом из которых по 2 элемента, т. е. на равномощные подмножества (рис.1). Кроме того, они попарно не передаются. В задаче спрашивается, сколько таких подмножеств получилось. Таким образом, число 4, полученное в ответе, – это число двухэлементных подмножеств, на которые разбито множество из 8 элементов.

Обратимся теперь к другой задаче: «12 карандашей раздали 3 ученикам поровну. Сколько карандашей получил каждый?»

Она также решается делением: 12:3=4 (карандаша). Но число 4 здесь выступает в другом смысле – как число элементов в каждом из трех равномощных непересекающихся подмножеств, на которые разбито множество, содержащее 12 элементов (рис.2).

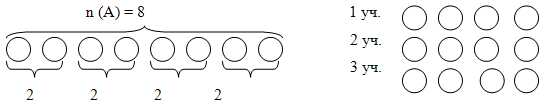
Рис. 1 Рис. 2

Иными словами, деление чисел связано с разбиением конечных множеств на равночисленные попарно непересекающиеся подмножества. При этом решаются две задачи: нахождение числа элементов в каждом подмножестве (деление на части) и нахождение числа таких подмножеств (деление по содержанию) [21,147].

В общем виде частное целого неотрицательного числа а и натурального числа b определяется следующим образом:

Определение. Пусть а=n(А) и множество А разбито на попарно непересекающиеся равномощные подмножества.

Если b – число подмножеств в разбиении множества А, то частным чисел а и b называется число элементов каждого подмножества.

Если b – число элементов каждого подмножества в разбиении множества А, то частным чисел а и b называется число подмножеств в этом разбиении [20,274].

Действие, при помощи которого находят частное а:b, называется делением, число а – делимым, b – делителем.

Часто, чтобы проверить правильность выполнения действия деления, мы обращаемся к умножению. Почему? Очевидно, потому, что действия деления и умножения взаимосвязаны. Но какова эта связь?

Пусть а =n (А) и множество А разбито на b попарно непересекающихся равномощных подмножества А1, А2, ., Аb. Тогда с = a:b есть число элементов в каждом таком подмножестве, т. е.

с = a:b = n (A1) = n (A2) = … = n (Ab).

Так как по условию

A=A1 A2 . Аb,

то n(А) = n (A1A2 .Ab).

Но подмножества А1, А2, ., Аb попарно не пересекаются, значит, по определению суммы

n(A1A2 .Ab) = n(A1) + n(A2) +…+ n(Ab) = с + с + . + с.

b слагаемых

Согласно определению произведения сумма b слагаемых, каждое из которых равно c, есть произведение с·b.

Таким образом, установлено, что а = с·b, т. е. частным чисел а и b является такое число с, произведение которого и числа b равно а. К такому же выводу мы придем, если частное с = а:b будет числом подмножеств в разбиении множества А.

Читайте также:

Средства формирования коммуникативной компетентности младших школьников
Задачей педагога, формирующего коммуникативную культуру, является установление дружеских связей у детей, развитие у них интереса ко всему происходящему, создание атмосферы доброжелательности, взаимного уважения и доверия, уступчивости и вместе с тем инициативности. Для достижения этого, на наш взгл ...

Работа над многозначными словами
Создание научной методики изучения явления много­значности диктуется нуждами школы. Мы сделали попытку экспериментально в процессе опытного обучения проверить: 1) соотношение индукции и дедукции в изучении полисе­мии; 2) сравнительную эффективность использования разных приемов работы в исследовател ...

Анализ опыта работы социального педагога с педагогически запущенными детьми
Социальный педагог - это должность, предназначенная для профессионала, компетентного специалиста, конкретного субъекта воспитательной системы. Он не похож на школьного учителя или другого работника образовательной системы. Ему приходится действовать непосредственно, в среде, окружающей личность – о ...