Введение понятий вектор, матрица

Пусть дан вектор на координатной плоскости. Как его можно записать? (Координатами (х,у).) А в пространстве? (x,y,z)А в каком пространстве живем мы? (4, (x,y,z,t)). Пара чисел (x,y) называется двухмерным вектором, тройка чисел (x,y,z) - трехмерным, (x,y,z,t)- четырехмерным. Их вводят для краткости записей и рассматривают как один элимент. Вектора можно обозначать, опять же для краткости.

В общем виде можно вектор можно записать так . Это n-мерный вектор. Вектора бывают и бесконечномерные, но их мы рассматривать не будем.

Задание 1.Приведите примеры векторов.

Каким образом записывают результаты футбольных матчей? (При помощи таблиц.)

Пусть в группе В играли пять команд по круговой системе. Результаты игры отображены в таблице.

Где 2- победа,1- ничья,0- поражение.

Эту таблицу также можно назвать матрицей.

Опр.Таблицу вида

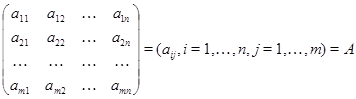
будем называть матрицей размерности .

Для краткости будем обозначать матрицы большими латинскими буквами.

Вектор является частным случаем матрицы при m=1.

Умножение матриц. Свойства

Как сложить две матрицы?

Опр.Суммой матриц и размерности называется матрица размерности .

Пример.

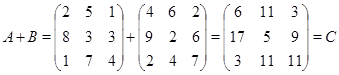
Как суммировать матрицы вы уже знаете. Теперь придумайте как умножить матрицу на число.

Опр.Произведением матрицы размерности и числа называется матрица размерности .

Пример.

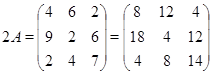
Кроме введенных операций нам понадобится умножение матриц.

Опр.Произведением матриц и называется матрица , где

Необходимо показать и озвучить практический способ умножения матриц: строка умножается на столбец. Берем первую строку матрицы А, ставим ее вертикально напротив первого столбца матрицы В, умножаем элементы этой строки и столбца, которые стоят напротив др.др., складываем произведения. Это первый элемент матрицы С. Теперь таким же образом умножаем эту строку на второй столбец - получаем второй элемент первой строки матрицы С. И т.д. Получим первую строку новой матрицы. Для того, чтобы получить вторую строку, проделываем тоже самое со второй строкой матрицы А.

Пример.

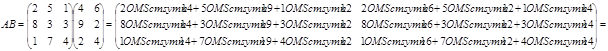
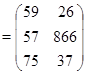
Задача 1.Выполнить умножение.

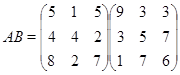
1.3.4 Домашнее задание

Задача 2.Выполнить умножение.

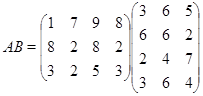
1.4 Четвертый урок

Опр.Замена строк матрицы на ее столбцы (а стольбцов на строки) называется транспонированием. Обозначается .

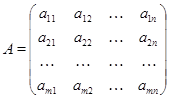
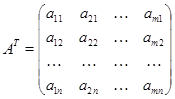
Пример.

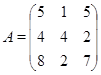
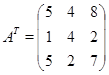
Определитель матрицы

Поставим каждой матрице по определенному правилу в соответствие число и назовем его определителем матрицы.

Читайте также:

Исторические предпосылки понимания педагогического процесса как целостного явления
Обращение к истокам возникновения педагогической профессии показывает, что стихийно протекавшие в ее рамках дифференциация и интеграция привели сначала к разграничению, а затем и к явному противопоставлению обучения и воспитания: учитель учит, а воспитатель воспитывает. Но уже к середине XIX в. в т ...

Пути реализации политехнического образования школьников
В процессе претворения в жизнь политехнического принципа в обучении школьников решается большой круг проблем. Политехническое образование в школе является одной из важнейших составных частей учебно-воспитательного процесса. При изучении основ наук учащиеся должны ознакомиться в теории и на практике ...

Система лексических упражнений
1. Здесь можно давать различные дефиниции одних и тех же слов. Однако важно помнить о том, что определение и есть исходный контекст употребления слова, его первичное окружение. Так, например, давая дефиниции к слову «стол», можно просто сказать: «Это то, за чем люди сидят во время еды», но можно и ...