Введение понятий вектор, матрица

Например:

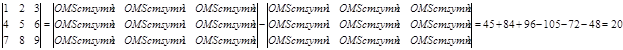
Таким образом вычисляют определители двхмерной и трехмерной матриц. Эта схема вычисления называется мнемоническим правилом. Для четырехмерной матрицы не удобно составлять такие схемы. Существует строгое правило нахождения определителя матрицы n-го порядка. Но мы будем работать только с трехмерными матрицами.

Необходимо обратить внимание на то, что матрица пишется в круглых скобках, а определитель матрицы - в прямых.

Задача 1.Найти определители матриц А и из Примера.

Обратить внимание, на то что определитель матрицы не совпадает с определителем транспонированной матрицы.

Задача 2.Найти определители матриц.

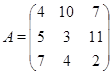
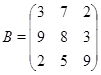
1.4.4 Домашнее задание

Задача 3.

Найти произведение матриц А и В из задачи 2. Вычислить определитель полученной матрицы.

Задача 4.

Найти значение выражения . Матрицы из задачи 2.

Необходимо сказать, что последовательность выполнения операций, такая же как и для чисел, но первым выполняют транспонирование.

1.5 Пятый урок

1.5.1 Проверка домашнего задания

1.5.2 Обратная матрица

Опр.Если , то обозначают и пишут .

Где - матрица с единицами на главной диагонали и нулями на остальных местах. Показать главную диагональ.

Для того, чтобы найти обратную матрицу нам необходимо найти т.н. алгебраическое дополнение.

Пусть дана матрица

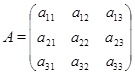
число

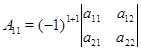
называется алгебраическим дополнением элемента . Алгебраическое дополнение можно найти для любого элемента матрицы.

Опр.Алгебраическим дополнением элемента называется произведение на определитель матрицы после вычеркивания из нее i-й строки и j-го столбца.

Теперь можно найти и обратную матрицу.

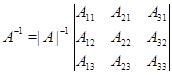
Задача 1.Найти обратную матрицу.

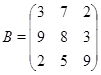
3.5.3 Домашнее задание

Задача 1.Найти обратную матрицу.

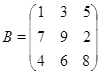
1.6 Шестой урок

1.6.1 Математическая постановка задачи

Итак, имеем две рисковые ц.б., заданные таблицей роста/падения цен и одну безрисковую, заданную процентом годовых. Необходимо сформировать портфель максимальной эффективности.

Доходность безрисковой ц.б. .

Если сегодня стоимость портфеля , а через год она окажется равной , то естественно назвать доходностью портфеля в процентах годовых. Т.е. доходность портфеля - это доходность на единицу стоимости.

Аналогично доходности всего портфеля находится доходность каждого вида акций. Т.е. нам нужно составить таблицу доходностей для ц.б. первого и второго видов. Например, для ц.б. первого вида доходность за первый год будет , за второй год - . Таким образом находим доходности за все 12 лет для каждого вида акций. Получаем таблицу с двумя столбцами и 11 строками.

Как правило, доходность бумаг колеблется во времени, так что будем считать ее случайной величиной. Найдем среднюю ожидаемую доходность и среднее квадратичное отклонение 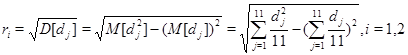И назовем их соответственно эффективностью и риском i-ой ценной бумаги. Эффективностью портфеля назовем . Т.е. математическое ожидание доходности портфеля.А величину (1) (где -ковариация i-ой и j-ой с.в.) назовем риском рисковой части портфеля портфеля.

Читайте также:

Специфика психологического восприятия студентами компьютерных технологий в обучении
Как известно, главное преимущество компьютерных технологий, особенно при выходе в Интернет, заключается в том, что любой человек получает доступ к максимально большому объёму знаний, полученных человечеством на данный момент в соответствующей области науки. Студент в принципе обеспечивается совреме ...

Методы обучения психологии
Учебные задачи представляют собой конкретизацию целей обучения, необходимую для подбора соответствующих методов и приемов. С их помощью определяется, чему именно должны научиться учащиеся. Интересный и конструктивный подход к классификации учебных задач был предложен В.Я. Ляудис (1989). Учебные зад ...

Анализ современного состояния дополнительного образования в Российской Федерации
Дополнительное образование детей является важнейшей составляющей образовательного пространства, сложившегося в современном российском обществе. Оно социально востребовано, требует постоянного внимания и поддержки со стороны общества и государства как образование, органично сочетающее в себе воспита ...