Введение понятий вектор, матрица

Обозначим - доля безрисковой ц.б. в портфеле. - вектор долей первой и второй ц.б. . Тогда естественно, должно выполнятся равенство . Пусть -ожидаемая эффективность бумаг. V- матрица ковариаций ценных бумаг. -риск портфеля.

Используя введенные обозначения, поставим математическую задачу. Как отмечалось выше: . Если возвести обе части равенства (1) в квадрат и записать в матричной форме, то получим . И теперь основное: необходимо добиться максимального значения эффективности портфеля, т.е. .

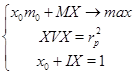
1.6.2 Решение задачи

Решение задачи найдем по формуле:

.

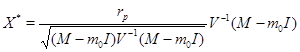В результате проделанных операций получим двухмерный вектор - доли рисковых акций в портфеле. Доля безрисковой акции в портфеле найдется из равенства .

Находить решение поставленной задачи удобнее разбив формулу по действиям. Если учащиеся хорошо усвоили предыдущий материал, то вычисления не вызовут ни каких затруднений, т.к. не содержат нового материла.

1.7 Седьмой урок

Напомнить результаты постановку математической задачи. Записать результ, к которому пришли на прошлом уроке. Продолжить решение.

Доли акций могут оказаться больше 1, или даже отрицательными. Если доля акции отрицательная - необходимо пройзвести операцию short sale. Суть этой операции состоит в следующем: инвестор, формирующий портфель, обязуется через какое-то время поставить бумаги i-го вида (вместе с доходом, который они принесли бы владельцу за это время). За это он сейчас получает их денежный эквивалент. Эти деньги он присоединяет к своему капиталу и покупает рекомендуемые оптимальным решением ц.б. Т.к. ценные бумаги других видов более эффективны, то инвестор оказывается в выигрыше. Можно обойтись и без операции short sale, если инвестору доступны займы денежных средств по безрисковой ставке. Тогда налагают дополнительное условие

В результате проделанной работы был составлен факультативный курс по теме "Оптимальный портфель ценных бумаг". Он позволяет учащимся профильных экономических классов глубже понять суть работы экономистов, увидеть тесную связь между математикой и экономикой, сделать профессиональный выбор. В ходе факультативных занятий школьники знакомятся с основными понятиями ТВиМС.

Факультатив содержит только необходимые для решения поставленной задачи (формирование оптимального портфеля Тобина максимальной эффективности из предложенных ценных бумаг) понятия. Однако, изученный материал позволяет сформировать у учащихся представление о ТВиМС.

Факультатив расчитан на 10, 11 профильные математические и экономические классы с высоким уровнем успеваимости. Проведенные в 10 экономическом классе МПГ №56 г.Гомеля занятия показали, что школьники способны усаваивать данный материал. Однако время уроков 2-6 необходимо увеличить до 2 академических часов.

Читайте также:

Экспериментальное использование современных информационных технологий как средства повышения познавательного интереса младших школьников
Для использования современных информационных технологий в учебном процессе мы: Обеспечили учебный процесс ноутбуками и мультимедиа-проекторами, Пополнили школьную медиатеку. Создали компьютерный методический кабинет для учителей и индивидуальной научно-исследовательской деятельности участников обра ...

Использование интеграции содержания учебных предметов для формирования ЗОЖ
Для успешного проведения интегрированных уроков необходимо создать атмосферу заинтересованности и творчества. В реализации межпредметных связей, при изучении биологии, условно можно выделить два блока процессов: актуализация и конкретизация. Под актуализацией мы понимаем создание на уроке такой сит ...

Нормативно-методические документы,регламентирующие правила создания и оформления документов
Основной объективной оценки образовательной деятельности Университета являются государственные стандарты. Университет в соответствии с лицензией, выданной в установленном законодательством Российской Федерации порядке, реализует следующие образовательные программы: программы высшего профессионально ...