Методика изучения квадратных уравнений

На третьем этапе рассматриваются приведенные квадратные уравнения, которые имеют вид х2 +px + q = 0 (3), где p и q - данные числа. Число p - коэффициент при х, а q - свободный член.

Дискриминант уравнения равен: D = p2 - 4q. Приведенные квадратные уравнения получаются из полного квадратного уравнения следующим образом:

Где и .

Рассматривают 3 случая:

1. D > 0, тогда уравнение (3) имеет два корня, вычисляемые по формуле

.

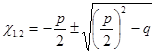(Приложение 1) (4)

2. D = 0, тогда уравнение (3) имеет единственный корень, или, как говорят, два совпадающих корня:

3. D < 0, то уравнение не имеет корней. Обычно в случае приведенного квадратного уравнения (3) вместо D рассматривается выражение , имеющее тот же знак, что и D. При этом формулу корней приведенного квадратного уравнения (4) записывают так:

Отсюда следует, что:

если то уравнение (3) имеет два корня;

если то уравнение имеет два совпадающих корня;

если то уравнение не имеет корней.

Важным моментом в изучении квадратных уравнений является рассмотрение теоремы Виета, которая утверждает наличие зависимости между корнями и коэффициентами приведенного квадратного уравнения [23,17].

Теорема Виета. Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену. (Приложение 2)

Иначе говоря, если x1 и x2 - корни уравнения х2 +px + q = 0, то

x1 + x2 = - p,

x1 x2 = q. (5)

Данные формулы называют формулами Виета в честь французского математика Ф. Виета (1540-1603), (Приложение 3) который ввел систему алгебраических символов, разработал основы элементарной алгебры. Он был одним из первых, кто числа стал обозначать буквами, что существенно развило теорию уравнений.

Например, приведенное уравнение х2 - 7х +10 = 0 имеет корни 2 и 5. Сумма корней равна 7, а произведение равно 10. Видно, что сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Справедлива также теорема, обратная теореме Виета.

Теорема, обратная теореме Виета. Если для чисел x1, x2, p, q справедливы формулы (5), то x1 и x2 - корни уравнения х2 + px + q = 0 [2,49].

Читайте также:

Технолого-экономические аспекты проблемы дистанционного обучения
Отставание России по количеству основного работоспособного населения в возрасте (25 - 60 лет), имеющего высшее образование усугубляется тяжелым положением образования в России вообще и высшего образования - в частности. Возросшее желание многих россиян наталкивается на ограниченные возможности вузо ...

Организация профессиональной ориентации учащихся 9-х классов в условиях школ и межшкольных комбинатов
Для формирования внутренней готовности учащихся к осознанному и самостоятельному определению в выборе профессии, корректировке и реализации своих профессиональных планов в условиях школ и межшкольных комбинатов проводится профессиональная ориентация учащихся. Рассмотрим особенности той и другой сто ...

Изобразительное искусство - основная составляющая эстетического воспитания дошкольников
Исследование особенностей восприятия детьми изобразительного искусства показало, что у детей уже в дошкольном возрасте проявляется интерес к различным видам и жанрам искусства, увлеченность рисованием, лепкой, аппликацией, развиваются познавательные потребности (как структурный компонент творческог ...