Разработка факультативного курса "Параметры в геометрии". Пояснительная записка

Заканчивается курс решением задачи Дидоны, которая упоминалась на первом вводном занятии. Эта задача решается только на примере прямоугольников для тех групп, которые проходят основной курс по учебнику Погорелова А. В. Другие примеры здесь рассматривать не целесообразно, так как учащиеся еще не знакомы с формулами площадей треугольников, четырехугольников, и др.

Для тех групп, которые проходят основной курс по учебнику Атанасяна Л.С. и др. задача Дидоны может быть рассмотрена на примерах треугольников и четырехугольников.

Содержание курса

1 занятие (вводная лекция)

Сам термин "параметр" в переводе с греческого означает "отмеривающий". Он обычно применяется в сочетании с другими математическими терминами, например, параметр уравнения, параметр неравенства, параметр функции и т.д. Под задачами с параметрами понимаются задачи, в которых технический и логический ход решения и форма результата зависят от входящих в условие величин, значения которых не заданы конкретно, но должны считаться известными.

Параметр- переменная величина, значение которой позволяет отличить один элемент некоторого множества от других элементов этого множества.

Под геометрическим параметром мы будем понимать любой элемент или элементы геометрической фигуры от величины, расположения или взаимного расположения которых зависит решение задачи, его существование или количество.

Примером одной из первых задач с параметром является знаменитая задача Дидоны. В IX в. до н.э. финикийская царевна Дидона, спасаясь от преследований своего брата, отправилась на запад вдоль берегов Средиземного моря искать себе прибежище, ей приглянулось одно место на побережье Тунисского залива. Дидона повела переговоры с местным предводителем Ярбом о продаже земли. Запросила она участок совсем небольшой — "столько, сколько можно окружить бычьей шкурой". Дидоне удалось уговорить Ярба, и сделка состоялась. Тогда Дидона изрезала шкуру быка на мелкие тесемки, связала их воедино и окружила большую территорию, на которой основала крепость и город Карфаген. Эта легенда содержится в поэме "Энеида" римского поэта Публия Вергилия Марона, а также в трактате "Об изопериметрических фигурах" древнегреческого ученого Зенодора, жившего между III в. до н.э. и началом н.э.

Задачу по отысканию среди всех замкнутых кривых с данным периметром той, которая охватывает максимальную площадь, называют задачей Дидоны.

Что же в этой задаче является параметром? Сформулируем задачу Дидоны в таком виде: "у какой фигуры Р, при заданном периметре, площадь будет наибольшей?". В данном случае параметром выступают не числовые данные, а фигура; при различных значениях этого параметра, то есть при различных фигурах задача будет иметь различные решения.

Математика оперирует строго определенными понятиями, а в окружающем нас мире на каждом шагу встречаются сплошные неопределенности, условности. "Если будет дождь, то праздник "День знаний" проходит по программе А, а если дождя не будет, то — по программе Б". Можно ли рассматривать условие "будет - не будет идти дождь" как параметр? Или математике нужны только числовые параметры? Для алгебры — это естественно. Но геометрия включает в себя не только числовые соотношения между фигурами или элементами фигуры, но и геометрические. Следовательно, для геометрии параметрами могут быть и классические "алгебраические" параметры, и сугубо специфические "геометрические" параметры.

В нашем курсе мы будем рассматривать задачи с геометрическими параметрами, а с некоторыми из них вы уже встречались в прошлом году:

1. Точки А, В и С лежат на одной прямой. Известно что АВ = 12см ВС = 13.5см. Какой может быть длина отрезка АС?

Из трех точек прямой одна и только одна лежит между двумя другими. Поскольку речь идет о трех точках, то каждая из них может лежать между двумя другими, и потому мы имеем три различных случая.

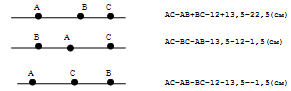
Отрицательное число не является решением, так как длина- положительное число.Ответ: 22,5см или 1,5см.

Известно, что АОВ = 35о, ВОС = 50о. Найдите угол АОС. Для каждого из возможных случаев сделайте чертёж с помощью линейки и транспортира.

Читайте также:

Функции педагогического общения
Педагогическое общение выполняет практически все основные функции, которые реализуются в обыденно-житейском непедагогическом общении. Наряду с этим функции педагогического общения имеют свои отличительные особенности (А.А. Лобанов). Информационная функция заключается в передаче через общение опреде ...

Содержание и условия сенсорного воспитания
Содержание сенсорного воспитания должно быть согласованно содержанием детской деятельности. Это значит, что обучение детей восприятию предметов, умению их анализировать, сравнивать должно быть согласованно с последующим процессом изобразительной, конструктивной или другой де4ятельности. В противном ...

Структура лексикона
Развитие психолингвистики и других наук о человеке стимулировало интерес к устройству словаря в голове индивида, функционирующего в соответствии с закономерностями психического развития человека ̶ носителя языка и культуры. Такой словарь принято называть ментальным или внутренним лексиконом че ...