Профилактика затруднений школьников при обучении математике на примере темы "Уравнения с переменной в знаменателе"

Однако, несмотря на простоту обоснования, второй способ более сложен, потому что при нем необходимо проверять изменения области определения уравнения при каждом преобразовании.

Итак, для решения таких уравнений используется 2 альтернативных метода, один – более алгоритмичен, но его обоснование не доступно ученикам, второй прост в обосновании, относительно сложен в реализации, но очень полезен при решении более сложных уравнений, когда учитываются не только нули знаменателя, но и область определения более сложных (тригонометрических, логарифмических, степенных, показательных) функций.

В качестве дополнительных упражнений, особенно для второго метода, необходимо включить в систему задач следующие:

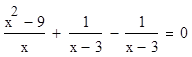
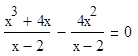
Подобные уравнения показывают, что необдуманное приведение подобных слагаемых или сокращение дроби приводит к расширению области определения.

Элементы тригонометрии, Рациональные неравенства, Системы уравнений

В этих темах широко используются методы решения рациональных уравнений, по этому, закрепление данной темы в основной школе происходит именно в этих разделах.

Уравнения с переменной в знаменателе – сложная для усвоения тема, она требует обширных знаний, умений и навыков в решении линейных уравнений, преобразованию многочленов и алгебраических дробей. Для её понимания необходимы навыки в выполнении таких заданий, как: найти множество допустимых значений переменной, упростить дробное выражение. Необходимым также является четкое понимание невозможности деления на 0.

Всё это достигается путем пропедевтики на этапе изучения соответствующих тем в 5-8 классах, периодическим повторением перечисленных вопросов, отработкой нужных навыков. Перечисленные рекомендации призваны помочь в организации этой работы.

Во время изучения данной темы существует несколько подходов к решению и теоретическому обоснованию алгоритма решения, выбор правильного подхода влияет как на понимание данной темы, так и на восприятие последующих тем и алгоритмов.

Применение навыков решения уравнений с переменной в знаменателе не ограничивается рассмотренными темами, они применяются во многих разделах в процессе дальнейшего изучения предмета. Поэтому, в дальнейшем также необходимо периодически обращаться к этому вопросу с целью повторения.

Читайте также:

Психолго-педагогические основы развития речи младших школьников
Одна из функций речи состоит в оформлении мысли, в ее выражении. «Внешняя речь,— как средство писал Л. С. Выготский,— есть процесс превращения мысли в слова, ее материализация» . Сле­довательно, психологической основой речи слу­жит мысль и условием ее развития является обогащение мысли. Лишь на осн ...

Влияние творческих занятий по предмету «Человек и мир» на развитие младших школьников
Курс «Человек и мир» обладает богатыми возможностями для экологического, морального и эстетического воспитания школьников «Именно в начальной школе нужно воспитывать у детей не потребительские отношения к окружающему миру, а партнерские, которые дают возможность гармонического сосуществования челов ...

Структурно-логическое содержание обучения - основа компьютерной технологии обучения
Для определения степени обучаемости студентов по каждой учебной дисциплине выделяют объем знаний, которые необходимы для усвоения согласно учебной программе, что составляет базовый объем знаний. Базовые знания представляют минимум государственного образовательного стандарта. Но и среди базовых знан ...