Профилактика затруднений школьников при обучении математике на примере темы "Уравнения с переменной в знаменателе"

Это задание требует знания определения дроби, в котором заложено отличие знаменателя от 0, правила деления дробей, а также факта невозможности деления на 0, доказанного в предыдущем пункте.

В качестве дополнительных заданий, а также для повторения темы «Дроби» можно использовать выражения вида:

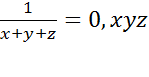
с формулировкой «Найти такие цифры x,y,z, что…».

Деление целых чисел

Тема изучается в 6 классе, по этому, требует повторения определения операции деления. Рекомендации те же, что для предыдущей темы – рассмотреть всевозможные случаи, в которых встречается 0, их, конечно, меньше, чем при делении дробей. Примеры: 0:2, 4:0, 0:0, обосновать результат, показать, почему на 0 делить нельзя.

Деление рациональных чисел

Тема схожа с делением дробей, с той разницей, что изучается она в 6 классе. Рекомендации те же, что в теме «Деление дробей».

Уравнения с 1 переменной и его корни

Не смотря на то, что случай переменной в знаменателе здесь еще не используется, следует обратить внимание учащихся на действия с уравнениями, а именно: «Если обе части уравнения умножить или разделить на одно и то же отличное от 0 число, то получится уравнение, равносильное данному».

Для закрепления можно использовать упражнения вида: «Равносильны ли уравнения»

Также следует уделить внимание предупреждению основных ошибок, встречающихся при работе с уравнениями, а именно:

При разложении на множители способом вынесения общего множителя за скобки один из полученных сомножителей всегда будет многочленом, состоящим из того же числа членов, что и данный. Пример ошибки: . Решение проблемы – подробное следование алгоритму разложения на множители.

С распределительным законом умножения относительно сложения связана ошибка такого рода: . Причина – перенос распределительного закона, связывающего умножение со сложением на связь деления со сложением.

Еще одна ошибка связана с применением ассоциативного закона к неассоциативным операциям: .

Возможность появления этих ошибок следует учитывать при работе со всеми видами уравнений, неравенств, а также с многочленами.

Функция, график функции: нахождение области определения функции

В этой теме необходимо пояснить нахождение области определения и вид графика функции при наличии переменной в знаменателе. Несмотря на то, что обратная пропорциональность и парабола еще не изучаются, их график школьники построить уже могут – с помощью таблицы.

Пример для рассмотрения: найти область определения функции и построить её график.

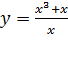
Область определения школьники найдут без труда, если перед этим актуализировать знания о делении и дробях, а с построением графика функции у них возникнут сложности. Решение проблемы:

Читайте также:

Работа с "трудными подростками"
Особое место в индивидуальной воспитательной работы мастера занимает работа с "трудными учащимися. Под трудными, педагогически запущенными учащимися подразумевается подростки, систематически нарушающие установленные нормы поведения в учебных заведениях и вне его, допускающие случаи правонаруше ...

Развитие коммуникативной компетентности в младшем школьном возрасте
коммуникативный компетентность умение школьник Младший школьный возраст – это оптимальный период активного обучения социальному поведению, искусству общения между детьми разного пола, усвоение коммуникативных и речевых умений, способов различения социальных ситуаций. Во-первых, с поступлением в шко ...

Психолого-педагогический аспект изобразительной деятельности детей раннего возраста в теоретической трактовке
Когда у ребенка возникают его первые рисунки, при каких обстоятельствах, почему он начинает рисовать, лепить? Ответы на эти вопросы мы находим у целого ряда исследователей. Наблюдения за первыми попытками ребенка рисовать, лепить, сделанные в разное время зарубежными авторами (В. Штерн, О. Шинн, X. ...