Профилактика затруднений школьников при обучении математике на примере темы "Уравнения с переменной в знаменателе"

Уравнения с 1 переменной и его корни: «Если обе части уравнения умножить или разделить на одно и то же отличное от 0 число, то получится уравнение, равносильное данному».

Нахождение корней линейного уравнения с 1 переменной: используется деление на не нулевой коэффициент.

Функция, график функции: нахождение области определения функции.

Пример:

Алимов Ш.А. «Алгебра 7»

Алгебраические равенства, формулы. Использование буквенных выражений:

Решение уравнений с одним неизвестным, сводящихся к линейным.

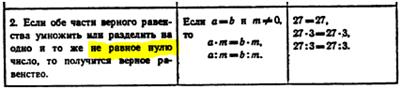
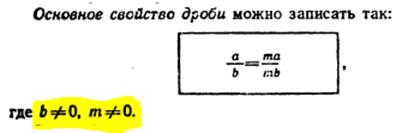
Алгебраическая дробь. Основное свойство дроби.

Функция, график функции. Тема не упоминается, понятие области определения не вводится.

Определение функции обратной пропорциональности для положительных Х. Неявное указание области определения.

Макарычев Ю. Н. «Аалгебра 7»

Выражения с переменными.

Далее приводятся задания для определения области допустимых значений переменной и нахождения значений переменных, при которых выражение не имеет смысла.

Уравнение с одной переменной: задания вида «укажите область определения уравнения»:

Функции и их графики. Область определения функции:

Пример задания:

Теляковский С. А. «Алгебра 8»

Рациональные дроби и их свойства.

Пример задания:

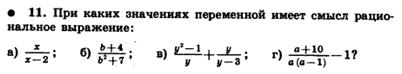
Сокращение дробей, основное свойство дроби:

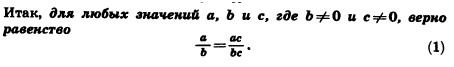
Деление дробей.

Функция .

Решение дробных рациональных уравнений

Пример задания:

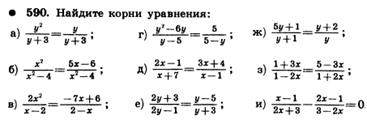
Мордкович А. Г. «Алгебра 8»

Алгебраические дроби. Основное свойство алгебраических дробей.

Читайте также:

Психолого-педагогические принципы деловой игры
Одной из приоритетных задач современной школы является создание необходимых и полноценных условий для личностного развития каждого ребёнка, формирование активной позиции каждого учащегося в учебном процессе. Поэтому использование активных форм обучения, например, деловой игры, является основой разв ...

Особенности изучения темы "Непредельные углеводороды" на уроках химии
В задачу изучения раздела "Непредельные углеводороды" входит закрепление на новом материале основных положений теории строения и рассмотрение понятий о кратных связях между атомами углерода и обусловливаемых ими химических свойствах органических соединений. Учащиеся узнают о новых типах х ...

Характеристика разнообразных форм уроков
Урок - логически законченный, целостный, ограниченных определенными рамками времени отрезок учебно-воспитательного процесса, где представлены все основные элементы этого процесса (цели, содержание, средства, методы, формы организации). Урок представляет собой форму организации деятельности учителя ...