Профилактика затруднений школьников при обучении математике на примере темы "Уравнения с переменной в знаменателе"

Случай деления на 0 не рассматривается.

Решение рациональных уравнений.

Гипербола, график гиперболы.

Случай 0 в знаменателе не рассматривается.

Алимов Ш. А. «Алгебра 9»

Функция, область определения функции.

Элементы тригонометрии. Пример применения темы:

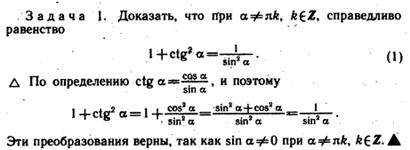
Повторение – решение уравнений. Примеры:

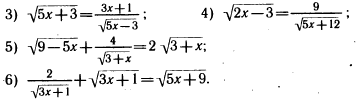
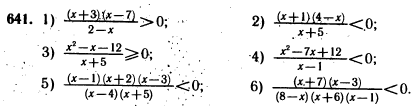
Мордкович А. Г. «Алгебра 9»

Рациональные неравенства

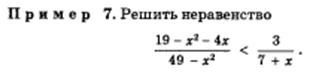
Системы уравнений

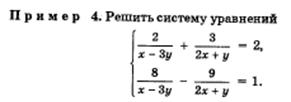
Функция, область определения

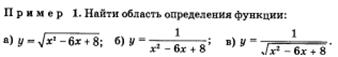
Функция и её график.

Тригонометрические функции.

Анализ приведенного материала

Проанализировав основные учебники, можно сделать вывод, что во всех учебниках 8 класса тема «рациональные уравнения» излагается довольно полно, однако, пропедевтика этой темы не приводится на достаточном уровне ни в одном учебнике. Отсюда у учащихся непонимание логики решения уравнений данного вида, формальный подход к их решению. Кроме того, в связи с частым использованием подобных уравнений в последующих темах, также необходимо повторение темы в 9 классе, которое в учебниках также мало представлено.

Темы, в которых затрагивается изучаемый раздел:

Введение операции деления

Изучение операций с дробями, основное свойство дроби.

Деление целых чисел

Деление рациональных чисел

Уравнения с 1 переменной и его корни

Функция, график функции: нахождение области определения функции

Выражения с переменными

Рациональные дроби и их свойства, деление дробей

Функция «обратная пропорциональность»

Решение дробных рациональных уравнений

Элементы тригонометрии

Рациональные неравенства

Системы уравнений

Обзор методов изучения темы

Метод - умножения дробей на их общий знаменатель.

Для примера решим дробное рациональное уравнение

(1)

Умножим обе части уравнения на общий знаменатель дробей, т е на выражение 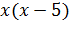. Получим целое уравнение

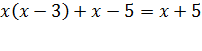.(2)

Понятно, что каждый корень уравнения (1) является корнем уравнения (2). Но уравнение (2) может быть не равносильно исходному, так как мы умножили обе его части не на число, отличное от нуля, а на выражение, содержащее переменную, которое может обращаться в 0. Поэтому каждый корень уравнения (2) обязательно окажется корнем уравнения (1).

Читайте также:

Методы индивидуального подхода
Процесс формирования привычных форм поведения, черт личности отличается некоторым своеобразным в зависимости от типа нервной системы учащегося. Для мастера-воспитателя далеко не безразлично, имеет ли он дело с учеником, относящимся к возбудимому. Спокойному или слабому типу нервной системы: безудер ...

Классификация методов обучения и воспитания
Методы обучения в их традиционных вариантах иногда подразделяют на методы преподавания (лекция, рассказ, показ-демонстрация, объяснение, беседа и др.), методы учения (слушание, осмысление, упражнение, изучение учебников и первоисточников, моделирование, в том числе практические работы, учебное иссл ...

Анализ современной социокультурной ситуации. Необходимость модернизации образования
Система образования, как важный институт социального и социо-культурного воспроизводства, призвана эффективно реагировать на изменения в системах общества и его культуры, поскольку эти изменения влекут за собой новые задачи и возможности, а, следовательно, требуют от молодых людей, включающихся в ж ...