Разработка факультативного курса "Параметры в геометрии". Пояснительная записка

Домашняя работа:

1. Найти высоту равнобедренного треугольника с основанием а и радиусом описанной окружности R.

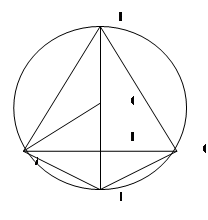
Решение.

Поскольку вершина, противолежащая основанию, может лежать на одной из двух дуг описанной окружности (т.е. в разных полуплоскостях относительно прямой, содержащей основание треугольника), то задача будет иметь два различных решения:

1) Если угол, противолежащий основанию, острый (В), то расстояние от центра окружности до основания ОМ=Н—R, где Н — высота ВМ, проведенная к основанию. Тогда по теореме Пифагора для треугольника АОМ: АО2=R2=()2+(H-R)2, откуда получаем квадратное уравнение относительно H: H2-2HR+=0. Корни этого уравнения числа

Н1,2=R±.

Если же угол, противолежащий основанию, тупой(Р), то расстояние от центра окружности до основания равно ОМ=R-Н, а следовательно, R2 = ()2+(R-H)2 что приведет к тому же самому квадратному уравнению. Таким образом, квадратное уравнение само предусмотрело два различных решения этой задачи.

Ответ: R±.

Задача Дидоны.(на примере прямоугольников). (для учащихся по учебнику Погорелова А.В.)

На последнем занятии посмотрим, какой все-таки участок приобрела Дидона. Легенда состояла в следующем:

В IX в. до н.э. финикийская царевна Дидона, спасаясь от преследований своего брата, отправилась на запад вдоль берегов Средиземного моря искать себе прибежище, ей приглянулось одно место на побережье Тунисского залива. Дидона повела переговоры с местным предводителем Ярбом о продаже земли. Запросила она участок совсем небольшой — "столько, сколько можно окружить бычьей шкурой". Дидоне удалось уговорить Ярба, и сделка состоялась. Тогда Дидона изрезала шкуру быка на мелкие тесемки, связала их воедино и окружила большую территорию, на которой основала крепость и город Карфаген.

Задачу по отысканию среди всех замкнутых кривых с данным периметром той, которая охватывает максимальную площадь, называют задачей Дидоны.

Задача Дидоны формулируется в таком виде: "у какой фигуры Р, при заданном периметре, площадь будет наибольшей?"

Допустим, что Дидона получила веревку, длиной р м.

Ей предложили на выбор несколько участков земли прямоугольной формы.

Это все участки прямоугольной формы с периметром р. Какой из них будет иметь наибольшую площадь?

Для начала, допустим, что верёвка получилась длиной 100м, тогда

Если одна из сторон – х, То другая- 50-х.

Подсчитав площадь, получим:

Х(50-х) = 50х-х2 = 625-(х2-50х+625) = 625-(25-х)2

Разность будет наибольшей, если (25-х)2=0, т.е х=25, т.е если четырехугольник- квадрат.

Теперь рассмотрим общий случай, когда периметр р.

Если одна из сторон – х, То другая- -х.

Подсчитав площадь, получим:

Х(-х) = х-х2 = ()2-(х2-х+()2) = ()2-(-х)2

Разность будет наибольшей, если (-х)2=0, т.е х=, т.е если четырехугольник - квадрат.

Таким образом получается, что из всех прямоугольников с одинаковым периметром наибольшую площадь имеет квадрат.

Читайте также:

Характеристика форм построения занятий
Процесс физического воспитания любого контингента населения (людьми разного возраста, пола, состояния здоровья и физической подготовленности) осуществляется путем последовательного проведения отдельных занятий физическими упражнениями. Являясь относительно самостоятельным звеном этого процесса, каж ...

«Современные подходы к проблеме игровой деятельности детей дошкольного возраста в психолого-педагогической литературе
Игра – один из видов человеческой деятельности. Как сложное и интересное явление издавна привлекает к себе внимание не только психологов и педагогов, но и философов, этнографов, искусствоведов, генетиков, писателей и т.д. В работах педагогов и психологов появились новые данные, подтверждающие, что ...

Уроки развития речи в системе изучения литературной темы
Хотя работа по развитию речи ведется в той или иной форме на каждом уроке литературы, наряду с ними проводятся и специальные уроки развития устной речи, на которых на материале изученного литературного произведения или нескольких произведений одного автора создается оптимальная ситуация речевого об ...