Разработка факультативного курса "Параметры в геометрии". Пояснительная записка

по теореме Пифагора в треугольнике О1МО2

О1М2=100к2-4х2

О1М=2

О1М=2О2Е

СО1=6к=СМ+МО1=ЕО2+МО1

6к= ЕО2+МО1=3О2Е

О2Е=2к

х=к

АВ=2к.

Ответ: 2к или 6к.

3. Периметр трапеции равен 112. Точка касания вписанной в трапецию окружности делит одну из боковых сторон на отрезки длины 8 и 18. Найдите основания трапеции.

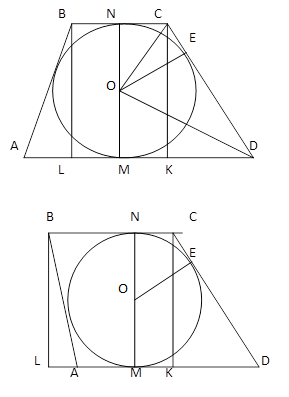
Решение: NC=CE=8, из равенства по гипотенузе и катету треугольников NOC и EOC. ED=MD=18, из равенства по гипотенузе и катету треугольников DOE и DOM. KD=MD-МК=18-8=10,

По теореме Пифагора для треугольника СКD:

СК= r=12

AB=BN+AМ (также как СD=NC+MD)

BN+AМ+AB=60(так как 112-8-8-18-18=60),

Тогда AB=30.

По теореме Пифагора для треугольника АВL:

AL=

1.P=AB+BN+NC+CD+DM+ML+AL=

=30+BN+8+26+18+ML+18=112

ML=BN=6, BC=8+6=14, AD=18+6+18=42.

P=AB+BN+NC+CD+DM+ML-AL=30+BN+8+26+18+ML-18=112

ML=BN=24, BC=24+8=32, AD=24-18+18=24.

Ответ: 14 и 42 или 24 и 32.

Домашняя работа:

1. Две стороны треугольника равны 25см и 30см. Найти третью сторону, если высота, проведённая к ней равна 24см.

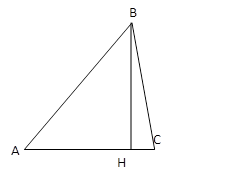
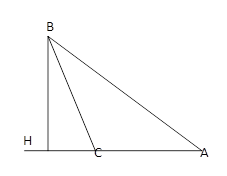
Решение:

АВ=30см, ВС=25см, ВН=24см.

Треугольники АВН и ВСН – прямоугольные.

По теореме Пифагора в АВН:

АН2=900-576=324

АН=18(см)

По теореме Пифагора в ВСН:

СН2=625-576=49

СН=7(см).

Поскольку не сказано, остроугольный или тупоугольный треугольник, то можно рассмотреть 2 случая:

остроугольный:

АС=АН+СН=18+7=25(см).

тупоугольный:

АС=АН-СН=18-7=11(см).

Ответ: 25см или 11см.

7 занятие( окружность и т Пифагора)

1. Длины соседних сторон вписанного в окружность четырехугольника отличаются на 1. Длина наименьшей из них так же равна I. Найдите радиус окружности.

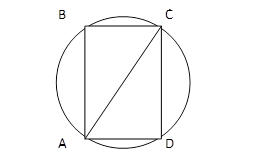
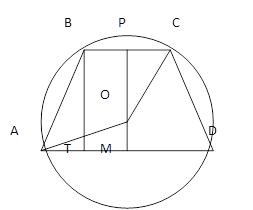
решение:

1) ВС=1, тогда АВ=ВС=2, АD=1

АС=

ОС=

2) ВС=1, тогда АВ=ВС=2, АD=3, к-радиус

ВТ=, пусть ОМ=а

По теореме Пифагора из тр-ка АОМ

К=

Из тр-ка ОРС:

К=

2.25=0.25+3-2а

а=, к=

ответ:

2. Дан отрезок длины 20. Три окружности с радиусами 4 имеют центры в концах отрезка или в его середине. Найдите радиус четвертой окружности, касающейся трех данных.

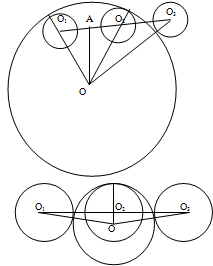
1. Решение: к-искомый радиус.

ОО1О2-равнобедренный, с боковыми сторонами, равными (к-4), тогда высота ОА является также и медианой.

По теореме Пифагора:

Из АОО2

ОА2=(К-4)2-25

Из АОО3

ОА2=(К+4)2-225

-8К-25=8К-225, 16К=200, К=12.5

2. пусть к- искомый радиус, ОО2=а, тогда к=4+а, по теореме Пифагора для треугольника ОО2О3

а2=((а+4)+4)2-100

16а=36,

а=2.25,

к=6.25.

Ответ: 6,25 или 12,5.

Читайте также:

Примеры ролевых игр
Игра “Коммивояжер” Дети всегда готовы играть и с нетерпением ждут объявления правил игры. Предлагаю им образовать фирмы, разбившись на группы по 3—4 человека. Все фирмы получают одно и тоже задание на программирование. Даже если учащиеся научились только составлять алгоритмы и записывать их на алго ...

Система упражнений, обеспечивающая усвоение таблицы умножения и деления
Табличные случаи умножения и соответствующие им случаи деления, учащиеся должны усвоить на уровне навыков. Основное средство выработки таких навыков – выполнение учащимися тренировочных упражнений. Если упражнения будут однотипными, повторяющимися, они могут вызвать потерю интереса у учащихся, поэт ...

Иерархия потребностной структуры ребенка в условиях социализации
Не одно десятилетие ученые и практики бились над положительным решением этой серьезной проблемы. Данные научных исследований в психологии раннего детства последних лет дали богатый материал, помогающие переосмыслить многие положения этой проблемы. Опыт практиков описывающих поведение детей в этот п ...