Разработка факультативного курса "Параметры в геометрии". Пояснительная записка

ВКА=КВС как внутренние накрест лежащие,

тогда АВК=ВКА=400, ВАК=1000.

А=1000, В=800, С=1000, К=800.

Получился параллелограмм, а по условию дана трапеция, значит такого случая быть не может.

Ещё одно решение получается, если рассмотреть трапецию, у которой при большем основании один угол острый, а другой – тупой.

ВС=ВК, АВ=ВК. А=400, тогда ВКА=400

ВКА=КВС как внутренние накрест лежащие, ВКС=С=700.

А=400, В=1400, С=700, К=1100.

Ответ: 400, 1400, 1000, 800 или 700, 1100, 1000, 800 или 400, 1400, 700, 1100.

3. Биссектрисы углов А и D параллелограмма АВСD пересекают прямую ВС в точках Е и F соответственно. Найдите стороны параллелограмма, если его периметр равен p и известно, что .

Решение: 1.рассмотрим сначала случай, когда точка пересечения биссектрис лежит внутри параллелограмма.

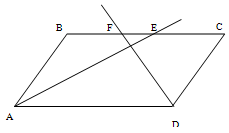
AB=BE=CF=CD, так как треугольники ABE и FDC равнобедренные, AD=CD как стороны параллелограмма, BAD=BEA Как внутренние Накрест лежащие при BC||AB и AC биссектриса.

Пусть EF=х

=AB+BE+FC-EF

=3BE-x=

Отсюда x=*.

AB=BE=

BC=BE+CF-x=.

2. теперь рассмотрим случай, когда точка пересечения биссектрис лежит вне параллелограмма.

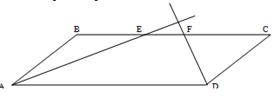
Здесь решение аналогично предыдущему: AB=BE=CF=CD аналогично.

Пусть

EF=x

=AB+BE+FC+EF

=3BE+x=

Отсюда х=

AB=BE=

BC=BE+CF+x=.

Ответ: если точка пересечения биссектрис лежит вне параллелограмма, то

AB= , BC=;

если точка пересечения биссектрис - внутри параллелограмма, то

AB=, BC=

Домашняя работа:

1. отношение углов А и В, прилежащих к боковой стороне трапеции АВСК, равно 2:3. диагональ АС делит трапецию на два равнобедренных треугольника. Найти углы трапеции.

Читайте также:

Технологии социальной работы
Выполняя различные социальные роли, специалист социальной работы реализует следующие функции: Образовательно-воспитательную – специалист обеспечивает целенаправленное педагогическое влияние на поведение и деятельность детей и взрослых, содействует образовательной и воспитательной работе всех социал ...

Организация образовательного процесса
3.1 Самостоятельно осуществляет образовательный процесс в соответствии с настоящим Уставом и лицензией. Обучение ведется на русском и татарском языках. 3.2 Образовательный процесс регламентируется учебным планом, разработанным и утвержденным ДДТ на основе примерных учебных планов и программ, курсов ...

Методика формирования познавательного интереса младших школьников в учебной и внеучебной деятельности по литературному чтению
Опытно-экспериментальная работа проводилась на базе средней школы №1 города Костаная. В эксперименте принимало участие 26 человек экспериментального 3 «В» класса и 26 человек контрольного 3 «А» класса. Целью эксперимента является проверка эффективности формирования познавательного интереса младших ...