Разработка уроков по теме "Приведенные квадратные уравнении

Урок - презентация по теме "Приведенные квадратные уравнения

Тип урока: изучение новой темы.

Цели: повторить понятие квадратного уравнения; ввести понятие приведенного квадратного уравнения; формировать умение распознавать квадратные уравнения и приводить к ним.

Ход урока:

Организационный момент.

Актуализация знаний.

Устный счет.

Устный опрос.

Какие уравнения называются квадратными? (Квадратное уравнение , a - старший коэффициент; b - второй коэффициент; c - свободный коэффициент (свободный член уравнения)).

Чему равен дискриминант квадратного уравнения?

Как найти корни полного квадратного уравнения?

Какие уравнения называются неполными?

Сколько корней имеет полное квадратное уравнение, если

а) D = 0; D < 0

б) D > 0

Сообщение темы и цели урока.

Объяснение нового материала.

Далее учитель объясняет новую тему.

Приведенное квадратное уравнение получается из квадратного уравнения по схеме:

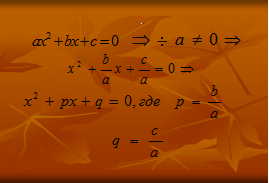
(Ученики делают записи в тетрадь)

Например, приведенными квадратными уравнениями являются уравнения:

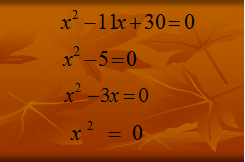
Таким образом, приведенное квадратное уравнение можно рассматривать как частный случай полного квадратного уравнения , где а = 1, b = p, c = q. Дискриминант уравнения равен: D = b

Обычно в случае приведенного уравнения вместо дискриминанта D рассматривается выражение . При этом формулу корней приведенного уравнения записывают так: .

5. Закрепление.

5.1 Решите уравнение:

1) (учитель решает у доски, учащиеся в тетрадях).

Читайте также:

Половое и гигиеническое воспитание в семье
Поскольку половое и гигиеническое воспитание, как и всякий другой вид воспитания – проблема педагогическая, то важную роль здесь должна играть семья и прежде всего – отец и мать. Семья играет главную роль в формировании личностных и эстетических ценностей у учащихся, является для них примером для п ...

Результаты экспериментальной проверки оптимальной модели обучения учащихся VII-VIII классов в процессе работы на токарно-винторезном станке
Экспериментальной базой квалификационной работы по проверке спроектированной модели процесса обучения учащихся VII-VIII классов работе на токарно-винторезном станке является СОШ № 5 п. Октябрьского Красноармейского района Краснодарского края. В педагогическом эксперименте принимали участие д. п. н. ...

Возрастные особенности учащихся 8 классов
Подростковый возраст - это возраст от 10 –11 до 15 лет, что соответствует возрасту учащихся 6-8 классов. Подростковый возраст называют переходным возрастом, потому что в течение этого периода происходит своеобразный переход (от детского к взрослому состоянию, от незрелости к зрелости). В этом смысл ...