Разработка уроков по теме "Приведенные квадратные уравнении

2) (1 ученик у доски, остальные в тетрадях).

3) ; (самостоятельно).

6. Итог урока.

Какие уравнения называются неполными, полными, приведенными?

Приведите примеры неполных, полных, приведенных квадратных уравнений.

Чем они отличаются?

7. Домашнее задание: теория, решить уравнения:

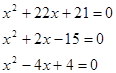
Урок - практикум по теме "Решение квадратных и приведенных квадратных уравнений"

Цели урока: отработка общих умений и навыков при решении квадратных уравнений; развитие внимания, навыков самоконтроля и самооценки.

Оборудование: карточки для самостоятельной работы, портрет ученого.

Ход урока:

1. Организационный момент (1 мин)

2. Сообщение темы и цели - повторим, то, что необходимо знать при решении квадратных уравнений; проверим свои умения решать квадратные уравнения в самостоятельной работе.

3. Разминка (6 мин)

3.1 Игра "Заполни квадрат". (Упражнение на развитие памяти и внимания). За 10 секунд запомнить, что записано в клетках квадрата, и записать в свой квадрат.

Расшифруйте слово. Зашифровано слово "УРАВНЕНИЕ"

3.2 Историческая справка. Простые уравнения люди научились решать более трех тысяч лет назад в Древнем Египте, Вавилоне и только 4000 лет назад научились решать квадратные уравнения. Одним из тех, кто внес большой вклад в развитие математики, был французский математик Виет. Имя этого математика нам скоро встретится.

4. Повторение (фронтальный опрос 6 мин)

4.1 Вычислите:

а) - 4*1* (-4), - 4*2*5, - 5*6*4;

б) (-10) 2, 3 2, (-7) 2

Это нужно уметь при нахождении дискриминанта D.

4.2 Игра "Срочная радиограмма". Класс делится на две команды: девочки - мальчики. В двух конвертах - отдельные слова. Задача: составить одно математическое предложение из имеющихся слов. Трудность состоит в том, что одного слова не хватает.

"Если дискриминант больше нуля, то уравнение имеет два различных корня";

"Если квадратное уравнение записано в стандартном виде, то можно находить дискриминант".

5. Тестовые вопросы (5 мин)

На доске 8 квадратных уравнений. Эти задания на слух, повторяются только два раза. Залог успеха - огромное внимание.

2х2 - 8х +4 = 0; 5.5х2+ 6х = 0;

3х2 + 4х - 1 = 0;

6. х2 - 8х + 12 = 0;

4х2 - 8 = 0; 7.3х2 = 0;

х2 - 10х + 100 = 0; 8.14 - 2х2 + х = 0

а) Выпишите номера полных квадратов уравнений.

б) Выпишите коэффициенты а, b, c в уравнении 8.

в) Выпишите номер неполного квадратного уравнения, имеющего один корень.

г) Выпишите коэффициенты a, b, c в уравнении 5.

д) Найдите дискриминант в уравнении 6.

е) Найдите дискриминант в уравнении 4 и сделайте вывод о количестве корней.

Проверяем, оцениваем себя сами:

нет ошибок - "5"

1 - 2 ошибки - "4"

3 - 4 ошибки - "3"

6. Игра " Следствие ведут знатоки " (10 мин)

Прежде чем доверить расследование серьезного дела, необходимо пройти проверку.

а) Сможете ли вы отыскать ошибку в решении уравнения?

- х2 + 6х + 16 = 0,х2 - 6х + 16 = 0,a = 1, b = - 6, c = - 16.

Читайте также:

Анализ психолого – педагогической литературы по проблеме педагогического общения
Общение – важнейший профессиональный инструмент педагогической деятельности. Исследования А.А. Бодалева, Н.В. Кузьминой, В.А. Канн – Калика, А.А. Леонтьева, А.Н. Мудрика, А. И Щербакова и других доказали большое значение общения в труде педагога. По мнению А.А. Лобанова, "общение" как жит ...

Все ли уроки личностно – ориентированны
Урок является многофункциональной единицей образовательного процесса, где сосредотачиваются и реализуются все педагогические воздействия; происходит общение учителя и учащихся, направ­ленное не только на активизацию познавательных возможностей, но и на систематическое, целенаправленное изучение лич ...

История возникновения деловой игры
Первая деловая игра была разработана и проведена в СССР в 1932 году М.М. Бирштейн. В 1938 году деловые игры в СССР постигла участь ряда научных направлений, они были запрещены. Их второе рождение произошло только в 60-х гг., после того как появились первые деловые игры в США (1956 г., Ч. Абт, К. Гр ...